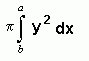Centre of Mass
The centre of mass (/gravity) of a body or a system of particles is the resultant of the weights of the individual particles making up the body or system.
Uniform Bodies
A uniform body is a body whose density is the same throughout the body. Finding the centre of mass of uniform bodies is relatively straightforward.
A lamina is a 2-dimensional object. In other words, it is a flat object whose thickness is we can ignore.
If a body has a line of symmetry, the centre of mass will lie on this line. This fact is very useful. For example, the centre of mass of a circular lamina is at the centre of the circle, since the centre of mass is on each axis of symmetry and they all meet at the centre.
Standard Results
-
The centre of mass of a uniform semicircular lamina of radius r lies on the axis of symmetry at a distance of 4r/3p from the straight edge
-
The centre of mass of a uniform solid right circular cone of height h lies on the axis of symmetry at a distance of h/4 from the base
-
The centre of mass of a uniform solid hemisphere of radius r lies on the axis of symmetry at a distance of 3r/8 from the base
Using Integration (M)
When the centre of mass of a body cannot be found using the axis/axes of symmetry, it can be found by integration.
Remember, from the definition of the centre of mass, it is the resultant of the weights of the individual particles making up the body. So we can take moments about any point and:
Moment of the total = the total of moments
In other words, (distance of centre of mass from O) × (weight of body) = the sum of: (the mass of each particle) × (the distance of each particle from O).
The "sum of" part can be replaced by an integral.
This might sound a bit confusing at first, but with practise it becomes second nature.
Another useful equation is: mass = density × volume
Example
Find the position of the centre of mass of a uniform semi-circular lamina, radius r.
We know that the centre of mass lies somewhere on the axis of symmetry of the semi-circle, although where on the axis of symmetry we do not know.
We therefore divide the semi-circle into many tiny strips, each with thickness dx.
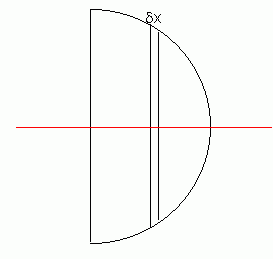
We know that the centre of mass lies on the red line, since this is a line of symmetry of the object.
If we label this line the x-axis and introduce a y-axis as follows, this will allow is to use calculus:
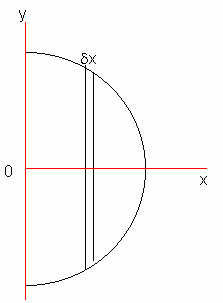
Each strip is a distance of x from the y-axis. The mass of each strip is its volume × density. The volume of each strip is just its area, since it is a lamina and so has no depth. The area of each strip is dx × 2y .
We are told that the body is uniform, which means that the density is constant. It doesn't matter what the density is, lets call it r. So the mass of each strip is 2y rdx.
Now the total area of the semicircle is ½ pr2 . So the total mass is ½ pr2r.
(distance of centre of mass from O) × (weight of body) = the sum of: (the mass of each particle) × (the distance of each particle from O)
Therefore: (centre of mass) × ½ pr2r = S 2y x r dx . The sum is from x = 0 to x = r .
(centre of mass) × ½ pr2r =
2y x r dx .
The integral is with respect to x, so we must replace the y by a function of x.
By thinking about similar triangles, we can deduce that y/r = x/r, so y = x
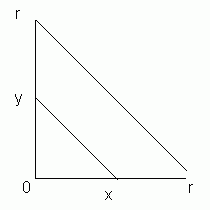
Therefore:
(Centre of mass) × ½ pr2r =
2x2 rdx
(Centre of mass) × ½ pr2r = (2r3 r)/3
So centre of mass is a distance of 4r/3p from O, on the axis of symmetry.
Solids of Revolution
If you are given the equation of a line, such as y = x2, the solid of revolution is the solid formed by rotating this line around an axis (usually the x-axis).
To find the centre of mass of such a body, use the technique similar to that in the above example. This time, however, remember that the body is not a lamina and so the volume does not equal the area. Also, instead of splitting the object into strips, split it into discs, each of thickness dx, radius y and distance x from the y-axis.
One very useful formula is:
-
Volume of solid of revolution =
Image