Motion in a Circle
This page covers Motion in a circle.
Angular Speed
Imagine an object is moving round a circular path.
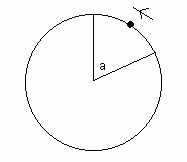
The angular speed is how fast the angle (which I have labelled "a") changes. So it measures how fast the object is moving round the circle.
Angular speed is usually measured in radians per second (rad s-1), which is how many radians the particle moves through in a second. Alternatively, it can be measured in revolutions per second, which is how many complete circles the object moves through in a second.
There is a formula connecting "normal" speed (usually called "linear speed") and angular speed:
- v = r w
where v is the linear speed, r is the radius of the circle and w is the angular speed.
Example
A particle is moving round a circle of radius 10cm. The angular speed is 2 rad s-1. Find the (linear) speed.
We want the radius in metres, which is 0.1m . Using the formula above, we get:
v = 0.1 × 2 = 0.2
So the speed is 0.2 m s-1 .
Note that if you are given the angular speed in terms of revolutions per second, you would have to convert to radians per second first. To do this, remember that 1 revolution per second is the same as 2p radians per second, because there are 2p radians in a circle.
Radial Acceleration
If a body is moving around a circle, even if it is moving at a constant speed it is accelerating. This is because it is changing direction (it isn't moving in a straight line).
The direction of this acceleration is towards the centre of the circle and the magnitude is given by:
- a = v2/r
where v is the speed and r is the radius of the circle.
Using our formula above, this can also be written as:
- a = r w2
Which of these you use will depend on whether you are dealing with speed or angular speed.
The acceleration occurs because there is a force acting:
Imagine that you are in a car going fast round a bend to the left. You will feel a force pulling you to one side (the left hand side). This is the force causing the acceleration. The force acts towards the centre of the circle.
Conical Pendulum
A conical pendulum looks a bit like this:
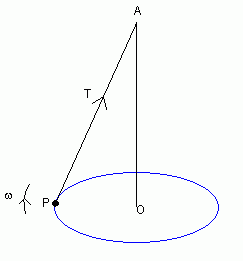
P is a particle. AP is a string. P is moving around the blue circle with angular velocity w.
Example
Suppose we have a conical pendulum as above, where the particle has a mass of 2 kg, the radius of the circle the particle moves in is 0.5 m and the angle at A is 45 degrees. Find the angular speed of P.
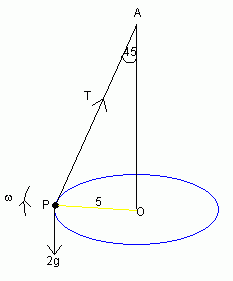
The weight is 2g (W= mg), where g is the acceleration due to gravity.
Resolving vertically: Tcos45 = 2g
Hence (√2T)/2 = 2g so T = 2√2 g (1)
Now use Newton's 2nd Law to find the equation of motion in the radial direction:
("F = m r w2")
Tsin45 = 2 × 5 × w2
Use (1) to eliminate T:
2√2 g × (√2)/2 = 10w2
g/5 = w2
So w = √(g/5)
Taking g = 9.8, we find that the angular speed is therefore 1.4 rad s-1
Motion on a Banked Surface
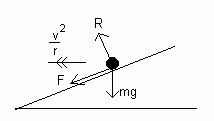
Now consider the motion of a particle round a "banked surface". By this, I mean a circular racing track, for example, which is sloped up from the centre to help the cars/bikes keep on the track at high speeds.
Now, if the car is going very fast, it would slip up the slope as it moves round the circle. If it is going slowly, it will slip down.
If the car has no tendency to slip, the forces and acceleration on the body will be as in this diagram (there is no frictional force):
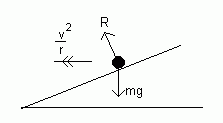
However, if the car was travelling faster, it would slip up the slope as it travels round the track. A frictional force would therefore act trying to prevent this happening:
The video below shows you how to convert radians and degrees.

