Motion in a Vertical Circle

This page looks at Motion in a Vertical Circle.

There are some problems when a particle is moving in a vertical circle, rather than a horizontal circle. In this case, gravity will be an important factor and the speed which the particle moves at will vary. As the particle gets higher, the speed will decrease.

If the particle is on the end of a string, it will continue to move in a circle as long as the string is taut. If the string becomes slack, however, the particle will start to behave as a projectile.

If the particle is on the end of a rod, if the speed reaches zero the particle will stop and fall back along from where it came.

Such problems are usually solved by applying the principle of conservation of energy. As the height of the particle increases, the potential energy increases but the kinetic energy decreases.

Example

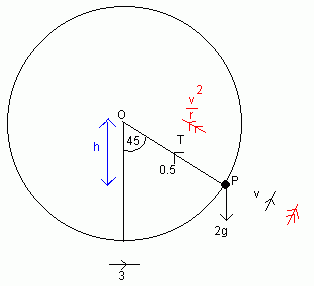
A particle P of mass 2kg is attached to the end of a light inextensible string, the other end of which is fixed at a point O. The length of the string is 0.5m . When the particle is hanging directly below O, it is projected horizontally with speed 3ms^-1. Find the speed of the particle and the tension in the string when the particle has moved through an angle of 45 degrees.

We're going to use conservation of energy, so we need to work out the initial energy:

Initial K.E. = "½ mv²" = ½ × 2 × 9 = 9

Initial P.E. = "mgh" = -2×g × 0.5 since initially the particle is 0.5m below O (hence the minus).

Final K.E. = 1/2 × 2 × v²

Final P.E. = -2gh where h is as labelled in the diagram

= -2g × 0.5 × cos45 = -½ g√2

So, by conservation of energy,

9 - g = v² - ½ √2g

v² = 6.1296...

v = 2.48 (3sf)

So the speed is 2.48 ms^-1 (3sf)

Now find the equation of motion in the direction PO ("F=ma"):

T - 2gcos45 =2v²/r

But we know that v² = 6.1296 and r = 0.5

Hence T = 24.518 + 13.859 = 38.4 (3sf)

So the tension is 38.4N (3sf)

Log in