Newton's Law of Restitution

Newton's Law of Restitution states that if two particles collide:

e (speed of approach) = (speed of separation)

where e is the coefficient of restitution .

Example

Particle A is travelling at 2m/s. Particle B is travelling in the opposite direction at a speed of 1m/s. After the particles collide, A is brought to rest. If the coefficient of restitution between the particles is ½, what will the speed of B be after the collision?

Let the speed of B after the collision be v (ms^-1).

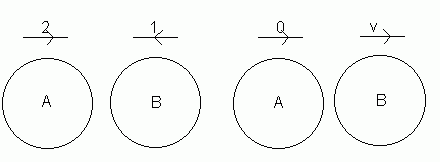
A and B are approaching each other at a speed of 3m/s (2 + 1)

Using Newton's Law of Restitution:

e(speed of approach) = (speed of separation)

½ (3) = v

Therefore the speed of B after the collision is 1.5ms^-1

Log in