Vectors

A vector quantity has both magnitude and direction. Acceleration, velocity, force and displacement are all examples of vector quantities. A scalar quantity has magnitude, so the direction is not important, (examples include speed, time and distance). A scalar can also have sign (such as work done and charge).

Vectors are usually represented as follows:

Image

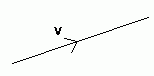
The arrow shows the direction and the number (v in this case) represents the magnitude.

Letters used to represent vectors should always be underlined or in bold type. For example, the velocity of an object may be represented by v. Since this is a vector quantity, it is in bold type. Small case letters are usually used to represent vectors.

Unit Vectors

A unit vector is a vector which has a magnitude of 1. There are three important unit vectors which are commonly used and these are the vectors in the direction of the x, y and z-axes. The unit vector in the direction of the x-axis is i, the unit vector in the direction of the y-axis is j and the unit vector in the direction of the z-axis is k.

Writing vectors in this form can make working with vectors easier.

For example, the vector 5i - 3j would look something like this on a diagram:

Image

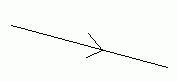
Adding Vectors

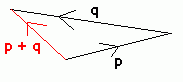
If two vectors are added together, the resultant is found by placing the vectors to be added end to end. If the vectors are given in unit vector form, you simply add together the i, j and k values.

Example

p = 3i + j, q = -5i + j. Find p + q.

Since the vectors are given in i, j form, we can easily calculate the resultant. 3i + j - 5i + j = -2i + 2j

This could also have been worked out from a diagram:

Image

The Magnitude of a Vector

The magnitude of a vector can be found using Pythagoras's theorem.

• The magnitude of ai + bj =  √(a² + b²)

Resolving a Vector

Resolving a vector means finding its magnitude in a particular direction.

Image

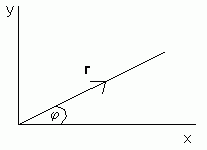
In the diagram above, the vector r has magnitude r and direction j to the x-axis. Using basic trigonometry, we can calculate that the component of r in the direction of the x-axis is rcosj. The component in the direction of the y-axis is rsinj. Therefore r = rcosji + rsinjj.

This video takes a look at Vectors and Scalars.