Functions
This section looks at functions within the wider topic of Algebra.
A function may be thought of as a rule which takes each member x of a set and assigns, or maps it to the same value y known at its image.
x → Function → y
A letter such as f, g or h is often used to stand for a function. The Function which squares a number and adds on a 3, can be written as f(x) = x2+ 5. The same notion may also be used to show how a function affects particular values.
Example
f(4) = 42 + 5 =21, f(-10) = (-10)2 +5 = 105 or alternatively f: x → x2 + 5.
The phrase "y is a function of x" means that the value of y depends upon the value of x, so:
- y can be written in terms of x (e.g. y = 3x ).
- If f(x) = 3x, and y is a function of x (i.e. y = f(x) ), then the value of y when x is 4 is f(4), which is found by replacing x"s by 4"s .
Example
If f(x) = 3x + 4, find f(5) and f(x + 1).
f(5) = 3(5) + 4 = 19
f(x + 1) = 3(x + 1) + 4 = 3x + 7
Domain and Range
The domain of a function is the set of values which you are allowed to put into the function (so all of the values that x can take). The range of the function is the set of all values that the function can take, in other words all of the possible values of y when y = f(x). So if y = x2, we can choose the domain to be all of the real numbers. The range is all of the real numbers greater than (or equal to) zero, since if y = x2, y cannot be negative.
One-to-One
We say that a function is one-to-one if, for every point y in the range of the function, there is only one value of x such that y = f(x). f(x) = x2 is not one to one because, for example, there are two values of x such that f(x) = 4 (namely –2 and 2). On a graph, a function is one to one if any horizontal line cuts the graph only once.
Composing Functions
fg means carry out function g, then function f. Sometimes, fg is written as fog
Example
If f(x) = x2 and g(x) = x – 1 then
gf(x) = g(x2) = x2 – 1
fg(x) = f(x – 1) = (x – 1)2
As you can see, fg does not necessarily equal gf
The Inverse of a Function
The inverse of a function is the function which reverses the effect of the original function. For example the inverse of y = 2x is y = ½ x .
To find the inverse of a function, swap the x"s and y"s and make y the subject of the formula.
Example
Find the inverse of f(x) = 2x + 1
Let y = f(x), therefore y = 2x + 1
swap the x"s and y"s:
x = 2y + 1
Make y the subject of the formula:
2y = x - 1, so y = ½(x - 1)
Therefore f -1(x) = ½(x - 1)
f-1(x) is the standard notation for the inverse of f(x). The inverse is said to exist if and only there is a function f-1 with ff-1(x) = f-1f(x) = x
Note that the graph of f-1 will be the reflection of f in the line y = x.
Graphs
Functions can be graphed. A function is continuous if its graph has no breaks in it. An example of a discontinuous graph is y = 1/x, since the graph cannot be drawn without taking your pencil off the paper:
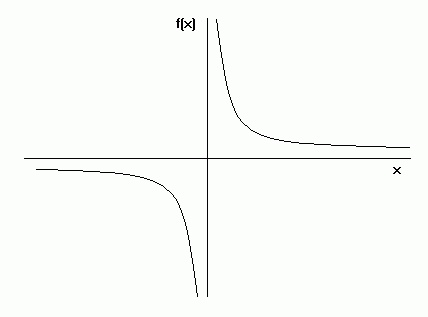
A function is periodic if its graph repeats itself at regular intervals, this interval being known as the period.
A function is even if it is unchanged when x is replaced by -x . The graph of such a function will be symmetrical in the y-axis. Even functions which are polynomials have even degrees (e.g. y = x²).
A function is odd if the sign of the function is changed when x is replaced by -x . The graph of the function will have rotational symmetry about the origin (e.g. y = x³).
The Modulus Function
The modulus of a number is the magnitude of that number. For example, the modulus of -1 ( |-1| ) is 1. The modulus of x, |x|, is x for values of x which are positive and -x for values of x which are negative. So the graph of y = |x| is y = x for all positive values of x and y = -x for all negative values of x:
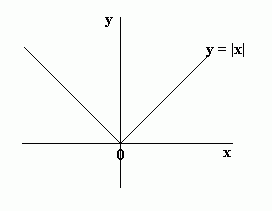
Transforming Graphs
If y = f(x), the graph of y = f(x) + c (where c is a constant) will be the graph of y = f(x) shifted c units upwards (in the direction of the y-axis).
If y = f(x), the graph of y = f(x + c) will be the graph of y = f(x) shifted c units to the left.
If y = f(x), the graph of y = f(x – c) will be the graph of y = f(x) shifted c units to the right.
If y = f(x), the graph of y = af(x) is a stretch of the graph of y = f(x), scale factor (1/a), parallel to the x-axis. [Scale factor 1/a means that the "stretch" actually causes the graph to be squashed if a is a number greater than 1]
Example
The graph of y = |x - 1| would be the same as the above graph, but shifted one unit to the right (so the point of the V will hit the x-axis at 1 rather than 0).
