Inequalities
When dealing with inequalities, it is important to remember that if you divide or multiply by a negative number, the direction of the inequality is changed.
When solving quadratic inequalities (inequalities with x2 in them), it is necessary to analyse the various cases to solve the inequality.
Example
Solve x2 + 3x + 2 > 0
Now, we can factorise the left hand side to get:
(x + 2)(x + 1) > 0
To solve this, we need to divide it up into a number of cases, based upon when the sign of one of the factors changes:
| x < -2 | -2 < x < -1 | x > -1 | |
| (x + 2) | negative |
positive |
positive |
| (x + 1) | negative |
negative |
positive |
| (x + 2)(x + 1) | positive |
negative |
positive |
So when x < -2, for example, we know that (x + 2) is less than 0 and (x + 1) is less than zero. Therefore (x + 2)(x + 1) > 0 (since negative times negative = positive).
From the table, therefore, (x + 2)(x + 1) > 0 when x < -2 or x > -1 .
Drawing a table like this makes things easier.
Alternatively, you can draw the graph of x2 + 3x + 2 > 0 and look at where the graph lies above the x-axis. You should get the same answer.
Linear Inequalities
Linear Inequalities can be solved by rearrangement in much the same way as linear equations. You must make sure however that you reverse the direction of the inequality when dividing or multiplying by a negative.
Example
Solve the inequality 8 – 3x > 23.
Subtract 8 from both sides of the equation: -3x > 15.
Divide both sides of the equation by -3: x < -5.
An Inequality which has x on both sides is treated like a corresponding equation.
Example
Solve the inequality 5x – 3 > 3x – 10.
Subtract 3x from both sides: 2x – 3 > - 10.
Add 3 to both sides: 2x > -7.
Divide both sides by 2: x > - 3.5
Quadratic Inequalities
If the quadratic expression cannot be factorised then the formula may be used to find the points of intersection of the curve with the x-axis.
Example
Solve the inequality x2 + 2x – 5 > 0.
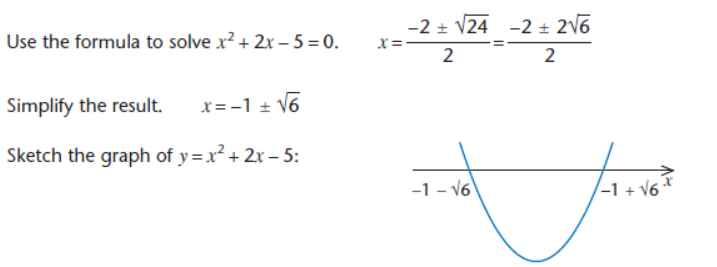
From the sketch above, x2 +2x – 5 > 0 when x < 1- √6 or when x > -1 + √6.
