Set Theory

This page covers Set Theory, Common Sets, Venn Diagrams, Intersections and Subsets.

A set is a group of objects. Each object is known as a member of the set. A set can be represented using curly brackets. So a set containing the numbers 2, 4, 6, 8, 10, ... is: {2, 4, 6, 8, 10, ... } . Sets are often also represented by letters, so this set might be E = {2, 4, 6, 8, 10, ...} . Alternatively, E = {even numbers} .

Common Sets

Some sets are commonly used and so have special notation:

Other Notation

Subsets

If A is a subset of B, then all of the elements of A are also in B. For example, if A = {1, 2, 3} and B = {1, 2, 3, 4, 5} then A Í B (Í means is a subset of).

Number of Members

If A = {1, 2, 4, 8}, then n(A) = 4. This is because n(A) means the number of members in set A.

The Universal Set

The universal set is the set of all sets. All sets are therefore subsets of the universal set.

Venn Diagrams

Venn diagrams are used to represent sets. Here, the set A{1, 2, 4, 8} is shown using a circle. In Venn diagrams, sets are usually represented using circles. The universal set is the rectangle. The set A is a subset of the universal set and so it is within the rectangle.

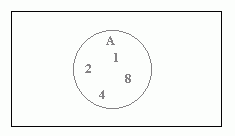
The complement of A, written A', contains all events in the sample space which are not members of A. A and A' together cover every possible eventuality.

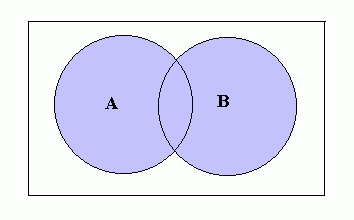
A ÈB means the union of sets A and B and contains all of the elements of both A and B. This can be represented on a Venn Diagram as follows:

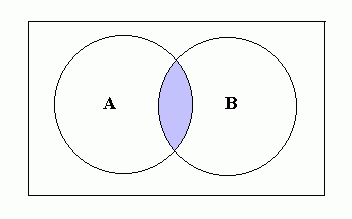
AÇB means the intersection of sets A and B. This contains all of the elements which are in both A and B. AÇB is shown on the Venn Diagram below:

An important result connecting the number of members in sets and their unions and intersections is:

n(A) + n(B) - n(AÇB) = n(AÈB)

Log in