Area Under a Curve
Calculating the area under a curve.
Definite Integrals
So far when integrating, there has always been a constant term left. For this reason, such integrals are known as indefinite integrals. With definite integrals, we integrate a function between 2 points, and so we can find the precise value of the integral and there is no need for any unknown constant terms [the constant cancels out].
Image
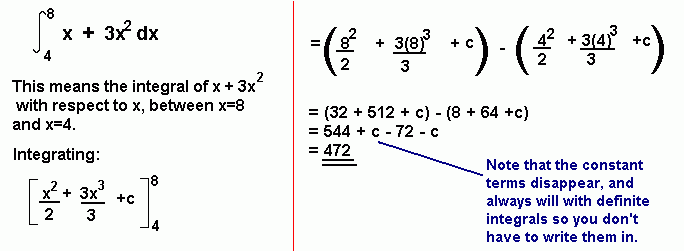
The Area Under a Curve
The area under a curve between two points can be found by doing a definite integral between the two points.
To find the area under the curve y = f(x) between x = a and x = b, integrate y = f(x) between the limits of a and b.
Image
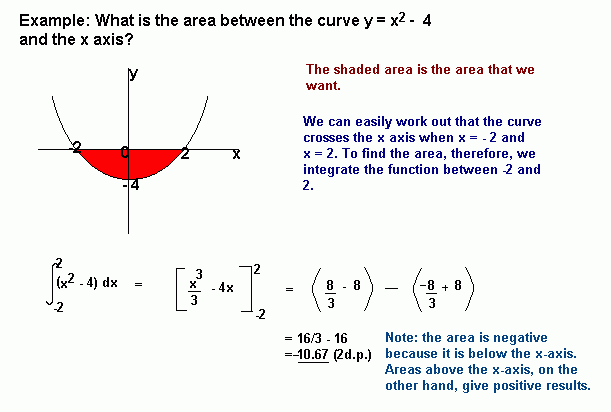
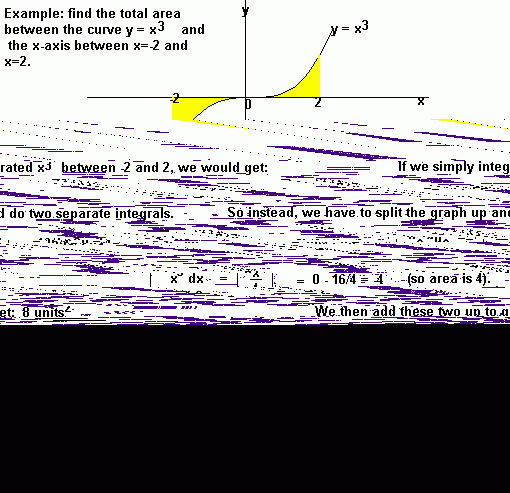
Areas under the x-axis will come out negative and areas above the x-axis will be positive. This means that you have to be careful when finding an area which is partly above and partly below the x-axis.
Image
You may also be asked to find the area between the curve and the y-axis. To do this, integrate with respect to y.
Example
Find the area bounded by the lines y = 0, y = 1 and y = x2.
Image
