Differential Equations
A differential equation is an equation which contains a derivative (such as dy/dx).
Example
To verify that something solves an equation, you need to substitute it into the equation and show that you get zero. So, here we need to work out dy/dx and show that this is equal to the right hand side when we substitute the x-3 into it.
dy/dx = -3x-4
and check that when you substitute x-3 into the right hand side you also get -3x-4.
Solving
When given a differential equation, you will often be asked to "solve" the differential equation or find the "general solution". This basically means find an expression which does not contain any derivatives. To do this you will need to integrate.
Example
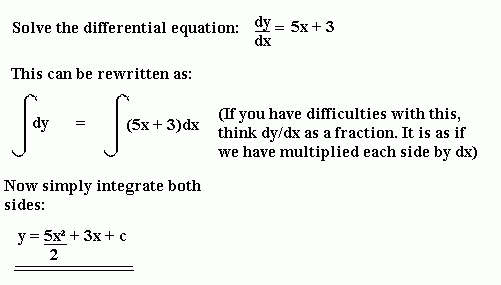
Initial or Boundary Conditions
You may be given information which allows you to work out the constant of integration.
In the above example, for example, you may have been told that y(0) = 0 [which means y = 0 when x = 0].
We can substitute these values into our answer to determine c:
0 = 0 + 0 + c, so c = 0
The answer in this case would therefore be y = 5x2/2 + 3x .
Forming Differential Equations
Using what you now know, you should be able to form simple differential equations from a statement.
Example
The velocity of a body is proportional to its distance from O. The body starts at 1.
If x is the distance from O, then the velocity is the rate of change of distance = dx/dt
Hence dx = ?k x, where k is the constant of proportionality
dt
Now, integrating gives us: ln x = kt + c
and we know that x(0) = 1, hence 0 = 0 + c
so ln x = kt
x = ekt

