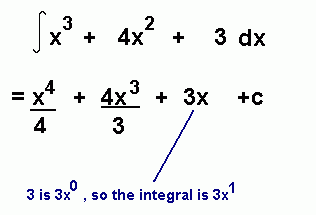Integration

Integration is the reverse of differentiation.

However:

If $y = 2x + 3, \frac{dy}{dx} = 2$

If $y = 2x + 5, \frac{dy}{dx} = 2$

If $y = 2x, \frac{dy}{dx} = 2$

So the integral of 2 can be $2x + 3, 2x + 5, 2x,$ etc.

For this reason, when we integrate, we have to add a constant. So the integral of $2$ is $2x$ + $c$, where c is a constant.

A $\int$ shaped symbol is used to mean the integral of, and $dx$ is written at the end of the terms to be integrated, meaning "with respect to $x$". This is the same "$dx$" that appears in $\frac{dy}{dx}$ .

To integrate a term, increase its power by $1$ and divide by this figure. In other words:

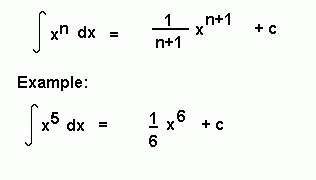
When you have to integrate a polynomial with more than $1$ term, integrate each term. So:

Log in