The Second Derivative
The second derivative is what you get when you differentiate the derivative. Remember that the derivative of y with respect to x is written dy/dx. The second derivative is written d2y/dx2, pronounced "dee two y by d x squared".
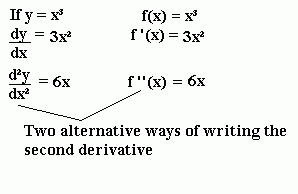
Stationary Points
The second derivative can be used as an easier way of determining the nature of stationary points (whether they are maximum points, minimum points or points of inflection).
A stationary point on a curve occurs when dy/dx = 0. Once you have established where there is a stationary point, the type of stationary point (maximum, minimum or point of inflexion) can be determined using the second derivative.
| If | d2y | is positive, then it is a minimum point |
| dx2 |
| If | d2y | is negative, then it is a maximum point |
| dx2 |
| If | d2y | = zero, then it could be a maximum, minimum or point of inflexion |
| dx2 |
If d2y/dx2 = 0, you must test the values of dy/dx either side of the stationary point, as before in the stationary points section.
Example
Find the stationary points on the curve y = x3 - 27x and determine the nature of the points:
At stationary points, dy/dx = 0
dy/dx = 3x2 - 27
If this is equal to zero, 3x2 - 27 = 0
Hence x2 - 9 = 0 (dividing by 3)
So (x + 3)(x - 3) = 0
So x = 3 or -3
d2y/dx2 = 6x
When x = 3, d2y/dx2 = 18, which is positive.
When x = -3, d2y/dx2 = -18, which is negative.
Hence there is a minimum point at x = 3 and a maximum point at x = -3.
