Coordinate Geometry
This section looks at Coordinate Geometry.
The Distance Between two Points
Draw a line between the two points. Complete a right angle triangle and use Pythagoras' theorem to work out the length of the line.
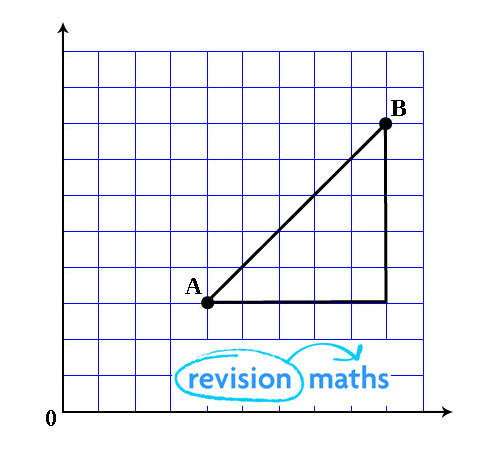
Between points A and B:
AB2 = (Bx – Ax)2 + (By – Ay)2
The Midpoint of a Line Joining Two Points
The midpoint of the line joining the points (x1, y1) and (x2, y2) is:
- [½(x1 + x2), ½(y1 + y2)]
Example
Find the coordinates of the midpoint of the line joining (1, 2) and (3, 1).
Midpoint = [½(3 + 1), ½(2 + 1)] = (2, 1.5)
The Gradient of a Line Joining Two Points
The gradient of a line joining points (x1, y1) and (x2, y2) is (y2 - y1)/(x2 - x1).
Parallel and Perpendicular Lines
If two lines are parallel, then they have the same gradient.
If two lines are perpendicular, then the product of the gradients of the two lines is -1.
Example
a) y = 2x + 1
b) y = -½ x + 2
c) ½y = x - 3
The gradients of the lines are 2, -½ and 2 respectively. Therefore (a) and (b) and perpendicular, (b) and (c) are perpendicular and (a) and (c) are parallel.
The Equation of a Line Using One Point and the Gradient
The equation of a line which has gradient m and which passes through the point (x1, y1) is:
- y - y1 = m(x - x1)
Example
Find the equation of the line with gradient 2 passing through (1, 4).
y - 4 = 2(x - 1)
y - 4 = 2x - 2
y = 2x + 2
Since m = y2 - y1
x2 - x1
The equation of a line passing through (x1, y1) and (x2, y2) can be written as:
y - y1 = y2 - y1
x - x1 x2 - x1
You can find information on geometry by clicking here
