Continuous Random Variables
A continuous random variable is a random variable where the data can take infinitely many values. For example, a random variable measuring the time taken for something to be done is continuous since there are an infinite number of possible times that can be taken.
For any continuous random variable with probability density function f(x), we have that:
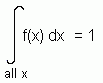
This is a useful fact.
Example
X is a continuous random variable with probability density function given by f(x) = cx for 0 ≤ x ≤ 1, where c is a constant. Find c.
If we integrate f(x) between 0 and 1 we get c/2. Hence c/2 = 1 (from the useful fact above!), giving c = 2.
Cumulative Distribution Function (c.d.f.)
If X is a continuous random variable with p.d.f. f(x) defined on a ≤ x ≤ b, then the cumulative distribution function (c.d.f.), written F(t) is given by:
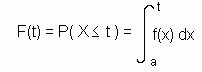
So the c.d.f. is found by integrating the p.d.f. between the minimum value of X and t.
Similarly, the probability density function of a continuous random variable can be obtained by differentiating the cumulative distribution.
The c.d.f. can be used to find out the probability of a random variable being between two values:
P(s ≤ X ≤ t) = the probability that X is between s and t. But this is equal to the probability that X ≤ t minus the probability that X ≤ s.
[We want the probability that X is in the red area:]
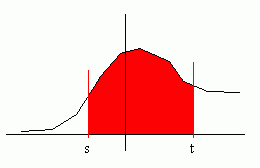
Hence:
-
P(s ≤ X ≤ t) = P(X ≤ t) - P(X ≤ s) = F(t) - F(s)
Expectation and Variance
With discrete random variables, we had that the expectation was S x P(X = x) , where P(X = x) was the p.d.f.. It may come as no surprise that to find the expectation of a continuous random variable, we integrate rather than sum, i.e.:
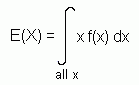
As with discrete random variables, Var(X) = E(X2) - [E(X)]2
