The Poisson Distribution

A discrete random variable X with a probability distribution function (p.d.f.) of the form:

Image

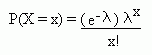
is said to be a Poisson random variable with parameter l. We write X ~ Po(l)

Expectation and Variance

If X ~ Po(l), then:

• E(X) = l.

• Var(X) = l.

Sums of Poissons

Suppose X and Y are independent Poisson random variables with parameters l and m respectively. Then X + Y has a Poisson distribution with parameter l + m. In other words:

• If X ~ Po(l) and Y ~ Po(m), then X + Y ~ Po(l + m)

Random Events

The Poisson distribution is useful because many random events follow it.

If a random event has a mean number of occurrences l in a given time period, then the number of occurrences within that time period will follow a Poisson distribution.

For example, the occurrence of earthquakes could be considered to be a random event. If there are 5 major earthquakes each year, then the number of earthquakes in any given year will have a Poisson distribution with parameter 5. 

Example

There are 50 misprints in a book which has 250 pages. Find the probability that page 100 has no misprints.

The average number of misprints on a page is 50/250 = 0.2 . Therefore, if we let X be the random variable denoting the number of misprints on a page, X will follow a Poisson distribution with parameter 0.2 .

Since the average number of misprints on a page is 0.2, the parameter, l of the distribution is equal to 0.2 .

P(X = 0) = (e^-0.2)(0.2⁰)

                       0!

= 0.819 (3sf)

Binomial Approximation

The Poisson distribution can be used as an approximation to the binomial distribution.

• A Binomial distribution with parameters n and p can be approximated by a Poisson distribution with parameter np.