Probability
The probability of an event occurring is the chance or likelihood of it occurring. The probability of an event A, written P(A), can be between zero and one, with P(A) = 1 indicating that the event will certainly happen and with P(A) = 0 indicating that event A will certainly not happen.
| Probability = |
the number of successful outcomes of an experiment |
|
the number of possible outcomes |
So, for example, if a coin were tossed, the probability of obtaining a head = ½, since there are 2 possible outcomes (heads or tails) and 1 of these is the ‘successful’ outcome.
Using Set Notation
Probability can be studied in conjunction with set theory, with Venn Diagrams being particularly useful in analysis.
The probability of a certain event occurring, for example, can be represented by P(A). The probability of a different event occurring can be written P(B). Clearly, therefore, for two events A and B,
-
P(A) + P(B) - P(AÇB) = P(AÈB)
P(AÇB) represents the probability of A AND B occurring. P(AÈB) represents the probability of A OR B occurring.
This can be shown on a Venn diagram. The rectangle represents the sample space, which is all of the possible outcomes of the experiment. The circle labelled as A represents event A. In other words, all of the points within A represent possible ways of achieving the outcome of A. Similarly for B.
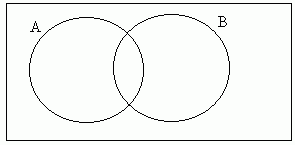
So in the diagram, P(A) + P(B) is the whole of A (the whole circle) + the whole of B (so we have counted the middle bit twice).
A" is the complement of A and means everything not in A. So P(A") is the probability that A does not occur. Note that the probability that A occurs + the probability that A does not occur = 1 (one or the other must happen). So P(A) + P(A") = 1. Thus:
-
P(A") = 1 - P(A)
Mutual Exclusive Events
Events A and B are mutually exclusive if they have no events in common. In other words, if A occurs B cannot occur and vice-versa. On a Venn Diagram, this would mean that the circles representing events A and B would not overlap.
If, for example, we are asked to pick a card from a pack of 52, the probability that the card is red is ½ . The probability that the card is a club is ¼. However, if the card is red it can"t be a club. These events are therefore mutually exclusive.
If two events are mutually exclusive, P(AÇB) = 0, so
-
P(A) + P(B) = P(AÈB)
Independent Events
Two events are independent if the first one does not influence the second. For example, if a bag contains 2 blue balls and 2 red balls and two balls are selected randomly, the events are:
a) independent if the first ball is replaced after being selected
b) not independent if the first ball is removed without being replaced. In this instance, there are only three balls remaining in the bag so the probabilities of selecting the various colours have changed.
Two events are independent if (and only if):
-
P(AÇB) = P(A)P(B)
This is known as the multiplication law.
Conditional Probability
Conditional probability is the probability of an event occurring, given that another event has occurred. For example, the probability of John doing mathematics at A-Level, given that he is doing physics may be quite high. P(A|B) means the probability of A occurring, given that B has occurred. For two events A and B,
-
P(AÇB) = P(A|B)P(B)
and similarly P(AÇB) = P(B|A)P(A).
If two events are mutually exclusive, then P(A|B) = 0 .
Independence
Using the above condition for independence, we deduce that if two events are independent, then:
P(A)P(B) = P(A|B)P(B) = P(B|A)P(A), or:
P(A) = P(A|B) and P(B) = P(B|A)
Example
A six-sided die is thrown. What is the probability that the number thrown is prime, given that it is odd.
The probability of obtaining an odd number is 3/6 = ½. Of these odd numbers, 2 of them are prime (3 and 5).
| P(prime | odd) | = | P(prime and odd) | = | 2/6 | = | 2/3 |
|
P(odd) |
3/6 |
