Functions

Functions and their graphs, after studying this section, you will be able to:

Functions

y = f(x) stands for 'y is a function of x'

When y = x² + 13 then f(x) = x² + 13

Therefore from the above f(x) + x = x² + 13 + x.

Transforming graphs of functions

What is the connection between the graphs of y = f(x) and y = f(x) + k?

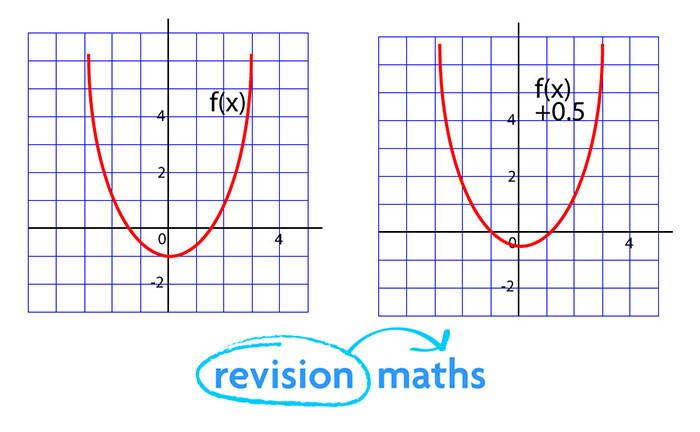
For every value of x, y = f(x) + k will be k more than y = f(x). The graph is translated on the y-axis by the value of k.

What is the connection between the graphs of y = f(x) and y = f(x+k)?

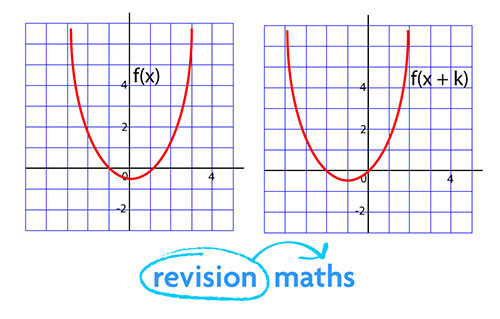
For every value of x, y = f(x + k) will take the value of x + k. The graph is translated on the x-axis by the value of -k.

What is the connection between the graphs of y = f(x) and y = kf(x)?

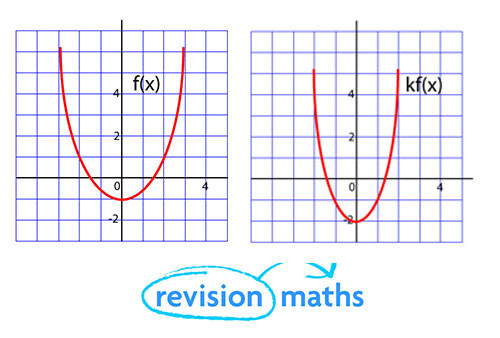
For every value of x, y will be k times larger. The graph is y=f(x) stretched along the y-axis by a the factor of k.

What is the connection between the graphs of y = f(x) and y = f(kx)?

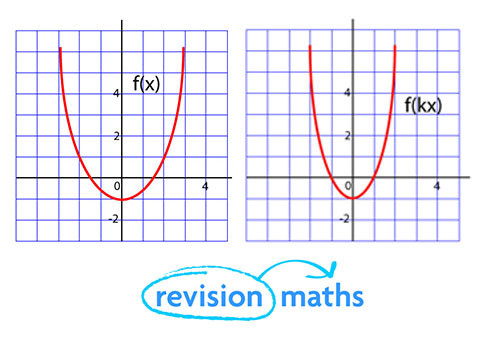
For every value of x, y takes the value it would have at kx. It is the graph of y = f(x) stretched by a factor of 1/k on the x-axis.

Log in