Gradients and Graphs
Gradient is another word for "slope". The higher the gradient of a graph at a point, the steeper the line is at that point. A negative gradient means that the line slopes downwards.
The video below is a tutorial on Gradients.
Finding the gradient of a straight-line graph
It is often useful or necessary to find out what the gradient of a graph is. For a straight-line graph, pick two points on the graph. The gradient of the line = (change in y-coordinate)/(change in x-coordinate) .
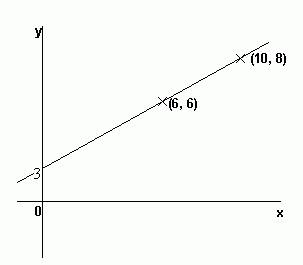
In this graph, the gradient = (change in y-coordinate)/(change in x-coordinate) = (8-6)/(10-6) = 2/4 = 1/2
We can, of course, use this to find the equation of the line. Since the line crosses the y-axis when y = 3, the equation of this graph is y = ½x + 3 .
Finding the gradient of a curve
To find the gradient of a curve, you must draw an accurate sketch of the curve. At the point where you need to know the gradient, draw a tangent to the curve. A tangent is a straight line which touches the curve at one point only. You then find the gradient of this tangent.
Example
Find the gradient of the curve y = x² at the point (3, 9).
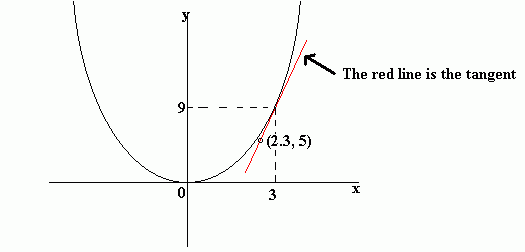
Gradient of tangent = (change in y)/(change in x)
= (9 - 5)/ (3 - 2.3)
= 5.71
Note: this method only gives an approximate answer. The better your graph is, the closer your answer will be to the correct answer. If your graph is perfect, you should get an answer of 6 for the above question.
Parallel Lines
Two lines are parallel if they have the same gradent.
Example
The lines y = 2x + 1 and y = 2x + 3 are parallel, because both have a gradient of 2.
Perpendicular Lines (HIGHER TIER)
Two lines are perpendicular if one is at right angles to another- in other words, if the two lines cross and the angle between the lines is 90 degrees.
If two lines are perpendicular, then their gradients will multiply together to give -1.
Example
Find the equation of a line perpendicular to y = 3 - 5x.
This line has gradient -5. A perpendicular line will have to have a gradient of 1/5, because then (-5) × (1/5) = -1. Any line with gradient 1/5 will be perpendicular to our line, for example, y = (1/5)x.
