Inequalities

This page covers solving inequalities after studying this section, you will be able to:

solve inequalities with one variable
solve inequalities with two variables

Inequalities: Quadratic Expressions

When you’re solving inequalities, it’s exactly the same as if you are solving algebraic equations. Let’s try and solve the following problem:

$$x^2 +4x + 1 < -2$$

Remember to treat the inequality sign as if it were an equals. This gives us $x^2 + 4x + 1 = –2$

The first thing you need to do is rearrange the inequality (equation) so it’s in the form $ax^2 + bx + c = 0$. All you have to do is bring the $–2$ to the left hand side.

This gives us $x^2 + 4x + 3 = 0$.

We can factorise this equation into two brackets: $(x + 3)(x + 1) = 0$

The solutions to this quadratic equation are $–3 and –1$.

Then we can think about sketching this equation:

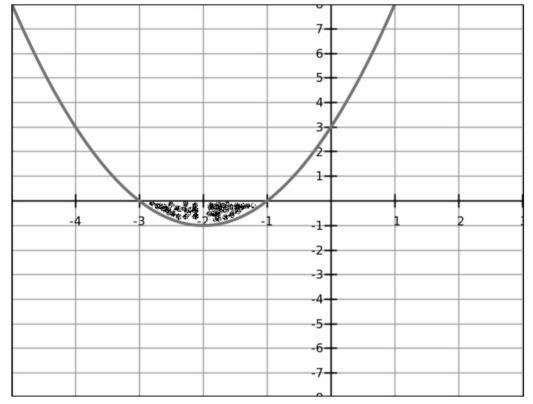
This is what the curve will look like if we drew it out (note the general U–shape as well).

Now we have to consider the original inequality. Remember the original inequality was this: $(x + 3)(x + 1) < 0$

This is the portion of the graph which lies below the line $y = 0$ (shaded).

That means the solution to this inequality is: $–3 < x < –1$

Think about what part(s) of the graph satisfy this inequality: $(x + 3)(x + 1) > 0$

Inequalities in one variable

≤ means 'less than or equal to'

≥ means 'greater than or equal to'

Inequalities can be shown on number lines.

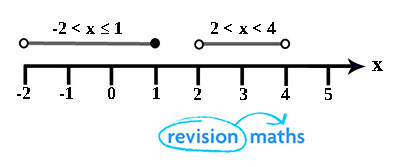
The 1st inequality covers the whole numbers -1, 0, 1. The 2nd inequality only covers 3.

The rules for manipulating inequalities are like those for equations except that multiplying or dividing each side by a negative number changes the direction of the inequality sign.

Examples:

a) Solve the inequality

$4(x-2) >x + 10$

$4x – 8 > x + 10$ (Expand the bracket)

$4x> x + 18$ (Add 8 to both sides)

$3x > 18$ (Subtract x from both sides)

$x> 6$ (Divide both sides by 3)

b) Solve

$1/3(4 – 4a) ≤ 8$

$4-4a ≤ 24$ (Multiply both sides by 3)

$-4a ≤ 20$ (Subtract 4 from both sides)

$-a ≤ 5$ (Divide both sides by 4)

$a ≥ -5$ (Multiply both sides by -1)

c) Find all the possible integer values of n that satisfy $3n + 1 ≤ 27 < 5n – 6$.

Splitting up the inequalities:

$3n + 1 ≤ 27$

$2n ≤ 26, n ≤ 8.66666 so n = 8, 7, 6, 5, …$

$27 < 5n – 6$

$33 < 5n, n > 6.6, so n = 7, 8, 9, …$

Integers that satisfy both are 7 and 8.

NOTE:

When working with a double inequalities start by solving the two inequalities. An integer is any whole number, positive negative or zero.

When solving inequalities do not forget that multiplying or dividing by a negative number reverses the inequality sign:

$−x > 3, becomes x < −3$(multiplying by −1).

Inequalities in two variables

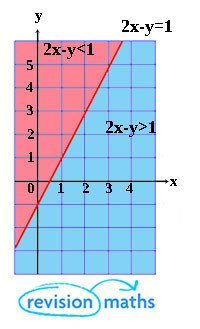
For an inequality in 2 variables: $2x - y > 1$.

Below is a graph for $2x-y = 1$. The formula can be rearanged as $y = 2x -1$ and results in a straight line.

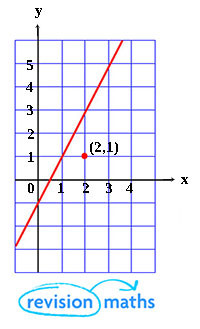
NOTE:Remember an equation in the form $y = 2x – 1$ has gradient $2$ and $y-$ intercept (where it crosses the y-axis) of –1,

in other words $y = (gradient) x + (y -intercept)$

The below graph shows the line of $2x-y=1$ while the area underneath the line covers values of $2x-y>1$ and the area above covers $2x-y<1$.

Several inequalities can be shown simultaneously.

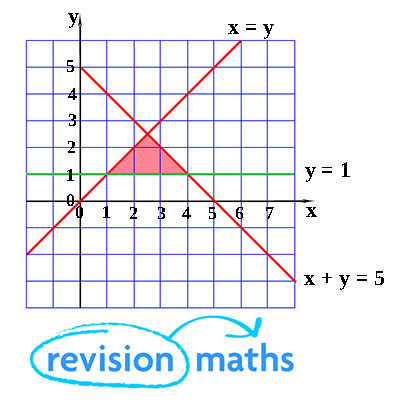
The shaded region satisfies $y ≤ x, x + y ≤$, and $y ≥ 1$.

Log in