Simultaneous Equations

Simultaneous equations and linear equations, after studying this section, you will be able to:

solve simultaneous linear equations by substitution
solve simultaneous linear equations by elimination
solve simultaneous linear equations using straight line graphs

If an equation has two unknowns, such as 2y + x = 20, it cannot have unique solutions. Two unknowns require two equations which are solved at the sametime (simultaneously) − but even then two equations involving two unknowns do not always give unique solutions.

The video below works through examples of simultaneous equations. The step-by-step example shows how to group like terms and then add or subtract to remove one of the unknowns, to leave one unknown to be solved.

This method is called solution by substitution.

It involves what it says − substitution − using one of the equations to get an expression of the form ‘y = …’ or ‘x = …’ and substituting this into the other equation. This gives an equation with just one unknown, which can be solved in the usual way. This value is then substituted in one or other of the original equations, giving an equation with one unknown.

NOTE:With this method you need to take particular care with your algebra. Should your solutions be ‘strange’ fractions such as 9/13 the chances are you’ve made a slip − check your algebra.

Example

Solve the two simultaneous equations:

2y + x = 8 [1]

1 + y = 2x [2]

from [2] y = 2x -1 ← subtract 1 from each side

Substituting this value for y into [1] gives:

2(2x – 1) + x = 8

4x – 2 + x = 8 ← expand the brackets

5x – 2 = 8 ←tidy up

5x = 10 ←Add 2 to each side

x = 2 ←By dividing both sides by 5 the value of x is found.

Substitute the value of x into y = 2x – 1 gives

y = 4 - 1 = 3

So x = 2 and y = 3

NOTE:

It is a good idea to label each equation. It helps you explain what you are doing − and may gain you method marks.
This value of x can be substituted into equation [1] or [2], or into the expression for y: y = 2x − 1.
Choose the one that is easiest!
As a check, substitute the values back into each of the two starting equations.

The second method is called solution by elimination.

NOTE:The method is not quite as hard as it first seems, but it helps if you know why it works.

It works because of two properties of equations:

Multiplying (or dividing) the expression on each side by the same number does not alter the equation.
Adding two equations produces another valid equation:

e.g. 2x = x + 10 (x = 10) and x − 3 = 7 (x also = 10).

Adding the equations gives 2x + x − 3 = x + 10 + 7 (x also = 10).

The object is to manipulate the two equations so that, when combined, either the x term or the y term is eliminated (hence the name) − the resulting equation with just one unknown can then be solved:

Here we will manipulate one of the equations so that when it is combined with the other equation either the x or y terms will drop out. In this example the x term will drop out giving a solution for y. This is then substituted into one of the otiginal equations.

Label your equations so you know which one your are working with at each stage.

Equation [1] is 2y + x = 8

Equation [2] is 1 + y = 2x

Rearrange one equation so it is similar to the other.

[2] y – 2x = -1

also 2 x [1] gives 4y + 2x = 16 which we call [3]

[2] y – 2x = -1

[3] 4y +2x = 16

[2] + [3] gives 5y = 15

so y = 3

substituting y = 3 into [1] gives 1 + (3) = 2x

so 2x = 4, giving x = 2 and y = 3

Solving simultaneous linear equations using straight line graphs

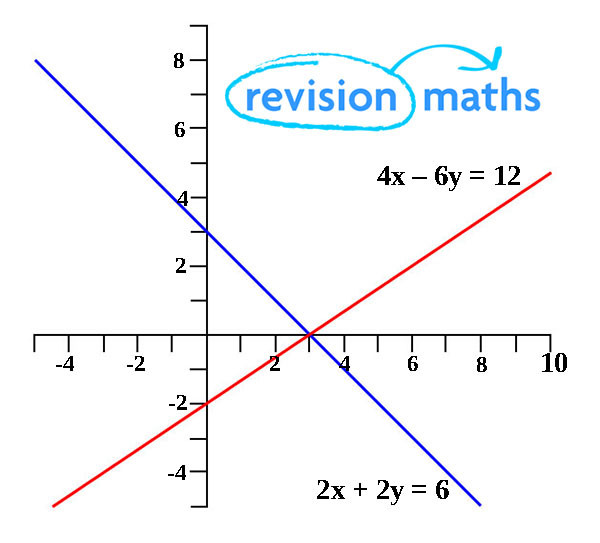
The 2 lines represent the equations '4x - 6y = -4' and '2x + 2y = 6'.

There is only one point the two equations cross.

Because the graphs of 4x - 6y = 12 and 2x + 2y = 6 are straight lines, they are called linear equations.

Note: Only draw a graph if the question asks you to, it is usually quicker to work out the point two simultaneous equtions cross algebraically.

Click here for more on solving equations.

Log in