Angle Theorems

Angle Theorems.

a) The angle at the circumference subtended by a diameter is 90°. This is usually stated as ‘The angle in a semicircle = 90°’.

This can be proved as follows:

• The lines OA, OP and OB are equal (radii of circle).
• Triangles and are isosceles.
• Therefore in triangle APB: a + a + b + b= 180°
• i.e. 2(a+b) = 180°
• therefore angle APB = a + b = 90° 

Image

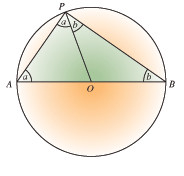
(b) The angle at the centre of a circle is twice the angle at the circumference.

Angle AOB = 2 x angle ACB

Image

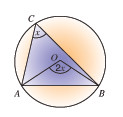
(c) Angles subtended by the same arc or chord are equal.

In Figure 1 the angles marked x are equal and subtended by chord CD, or arc CD.

Image

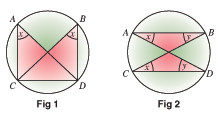
In Figure 2 the angles marked x are equal, being subtended by chord BD and the angles marked y are equal, being subtended by chord AC.

Examples

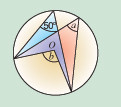
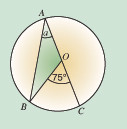
(a) In this diagram O is the centre of the circle. Calculate the value of angle a.

Angle a = 37.5° (angle at the centre = 2 x angle at the circumference)

Image

(b) Calculate the angles marked with letters. angle a = 50° (angles subtended by the same arc)

angle b = 100° (angle at centre  twice angle at circumference)

Image