Loci

This section covers Loci within Geometry and Measures.

A locus is a set of points satisfying a certain condition. For example, the locus of points that are 1cm from the origin is a circle of radius 1cm centred on the origin, since all points on this circle are 1cm from the origin.

N.B. if a point P is ‘equidistant’ from two points A and B, then the distance between P and A is the same as the distance between P and B, as illustrated here:

Image

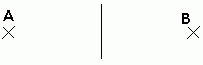
The points on the line are equidistant from A and B

Don’t let the term 'locus' put you off. Questions on loci (which is the plural of locus) often don’t use the term.

Example

The diagram shows two points P and Q. On the diagram shade the region which contains all the points which satisfy both the following: the distance from P is less than 3cm, the distance from P is greater than the distance from Q.

Image

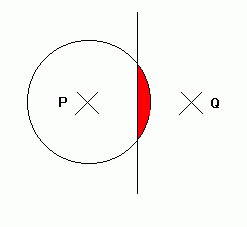
All of the points on the circumference of the circle are 3cm from P. Therefore all of the points satisfying the condition that the distance from P is less than 3cm are in the circle.

If we draw a line in the middle of P and Q, all of the points on this line will be the same distance from P as they are from Q. They will be therefore closer to Q, and further away from P, if they are on the right of such a line.

Therefore all of the points satisfying both of these conditions are shaded in red.

Three important loci

The word locus describes the position of points which obey a certain rule.

Three important loci are:

• The circle - the locus of points which are equidistant from a fixed point, the centre.
• The perpendicular bisector - the locus of points which are equidistant from two fixed points A and B.
• The angle bisector - the locus of points which are equidistant from two fixed lines.

Example:

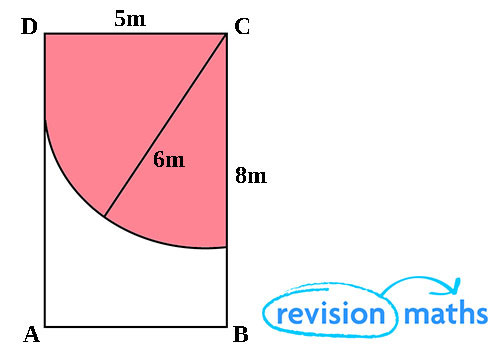
The diagram shows the walls of a rectangular shed, ABCD, measuring 8m by 5m. A goat is tied to the corner of C by a rope 6m long.

The shaded area shows the part the goat can reach.

Image