Transformations

This section covers transformations, enlargements, rotations and reflections.

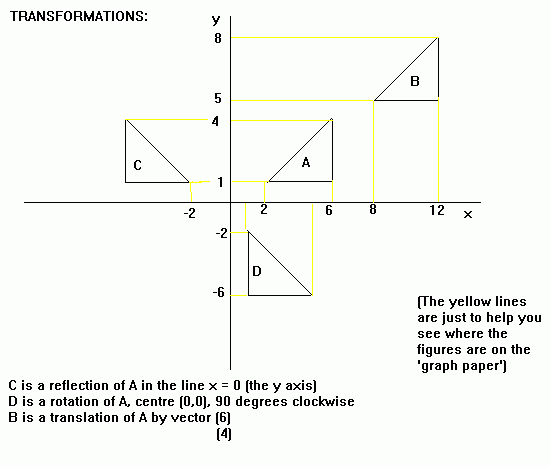
A translation occurs when a shape is moved from one place to another. It is equivalent of picking up the shape and putting it down somewhere else. Vectors are used to describe translations.

The video and text below looks at Translations including: Reflections, Rotations and Enlargements. 

Reflections

A reflection is like placing a mirror on the page. When describing a reflection, you need to state the line which the shape has been reflected in. The distance of each point of a shape from the line of reflection will be the same as the distance of the reflected point from the line.

For example, below is a triangle that has been reflected in the line y = x (the length of the pink lines should be the same on each side of the line y=x):

Image

Rotations

When describing a rotation, the centre and angle of rotation are given. If you wish to use tracing paper to help with rotations: draw the shape you wish to rotate onto the tracing paper and put this over shape. Push the end of your pencil down onto the tracing paper, where the centre of rotation is and turn the tracing paper through the appropriate angle (if you are not told whether the angle of rotation is clockwise or anticlockwise, it would usually be anticlockwise). The resultant position of the shape on the tracing paper is where the shape is rotated to.

Image

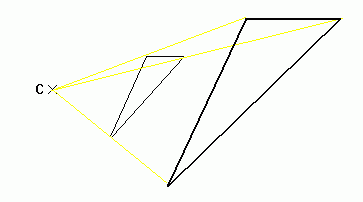
Enlargements

Enlargements have a centre of enlargement and a scale factor.

1) Draw a line from the centre of enlargement to each vertex ('corner') of the shape you wish to enlarge. Measure the lengths of each of these lines.

2) If the scale factor is 2, draw a line from the centre of enlargement, through each vertex, which is twice as long as the length you measured. If the scale factor is 3, draw lines which are three times as long. If the scale factor is 1/2, draw lines which are 1/2 as long, etc.

Example

The centre of enlargement is marked. Enlarge the triangle by a scale factor of 2.

Image