Vectors

Calculating the Modulus of a Vector

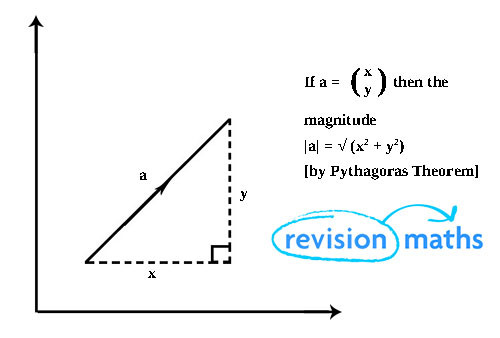
In this section, you will learn how to calculate the modulus of a vector. The modulus is a mathematical term for the length or the magnitude.

This video and text below takes a look at Vectors and Scalars.

The magnitude of vector x is written as |x|.

The magnitude of vector

is written as |AB|.

Zero vector and unit vectors

A vector with magnitude 0 is called the zero vector, written 0. A vector with magnitude 1 is called a unit vector.

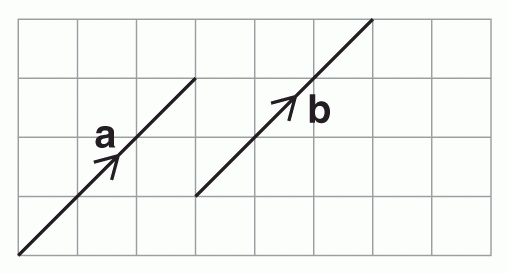
Vectors are equal if they have the same magnitude and the same direction.

a = b

Inverse Vectors

The inverse of a vector is a vector of equal magnitude but in the opposite direction. The inverse of

is -

or

and the inverse of a is -a.

Scalars

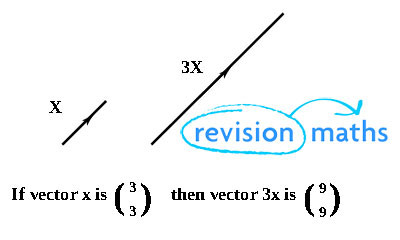
Scalars have magnitude but not direction. Vectors can be multiplied by a scalar to produce another vector.

Multiplying vector x by 3 will give a new vector 3 times the length and parallel to x.

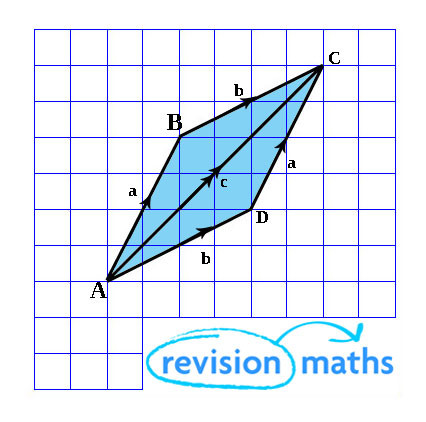
Vector addition and subtraction

When 2 vectors are added or subtracted the vector produced is called the resultant.

The resultant is identified by a double arrowhead.

Triangle Law:

To add two vectors you apply the first vector and then the second.

+

=

or

a + b = c

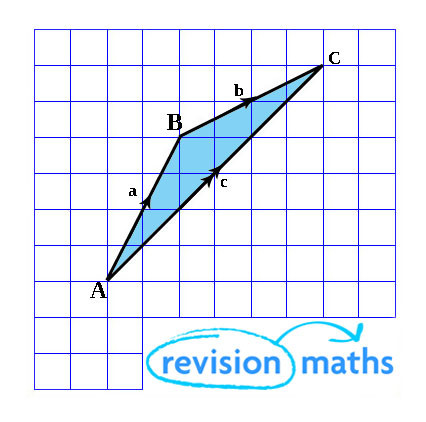
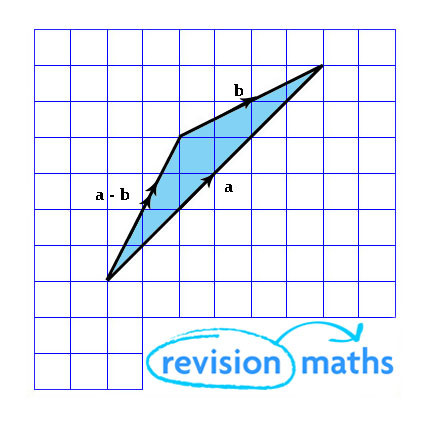
Subtracting a vector is the same as adding its inverse.

a – b is the same as a + (-b)

Parallelogram Law:

Moving from A to C through B is the same as moving through D.

+

=

+

=

or

a + b = b + a = c

Log in