Bearings

A bearing is an angle, measured clockwise from the north direction. Below, the bearing of B from A is 025 degrees (note 3 figures are always given). The bearing of A from B is 205 degrees.

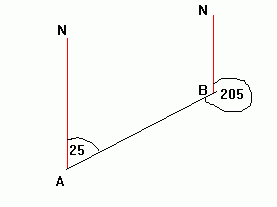
Example

A, B and C are three ships. The bearing of A from B is 045º. The bearing of C from A is 135º. If AB= 8km and AC= 6km, what is the bearing of B from C?

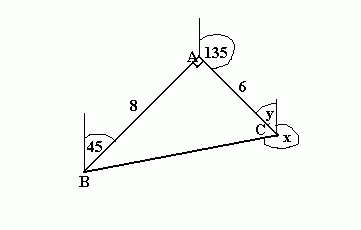
tanC = 8/6, so C = 53.13º

y = 180º - 135º = 45º (interior angles)

x = 360º - 53.13º - 45º (angles round a point)

= 262º (to the nearest whole number)

This video shows you how to work out Bearings questions.

Sample GCSE Style Question:

A hiker walks from point A on a bearing of 060° for 2 kilometres to point B. From point B, the hiker changes direction and walks on a bearing of 150° for 3 kilometres to point C. Determine:

a) The bearing of point A from point C. b) The distance between point A and point C, to the nearest kilometre.

Answer:

a) To find the bearing of point A from point C, we first calculate the bearing from C to A, which is the opposite direction from the bearing from A to C. The bearing from C to A is 180° different from the bearing from A to C.

Bearing from C to A = 150° + 180° = 330°

So, the bearing of point A from point C is 330°.

b) To find the distance between point A and point C, we can use the sine rule. First, we'll find the angle CAB using the fact that the sum of angles in a triangle is 180°.

Angle CAB = 180° - (60° + 150°) = 30°

Now, we can use the sine rule:

sin(CAB) / AC = sin(ABC) / BC

sin(30°) / AC = sin(90°) / 3 (as angle ABC is a right angle)

sin(30°) / AC = 1 / 3

AC = sin(30°) * 3

AC ≈ 1.5 kilometres

So, the distance between point A and point C is approximately 1.5 kilometres.

Log in