Congruency

This page covers congruency and congruent triangles.

Two shapes are congruent if they are the same (shape and size)- in other words, if the lengths of the sides and the angles are the same. It is often useful to know when two triangles are congruent.

Two triangles are congruent if any one of the following is true:

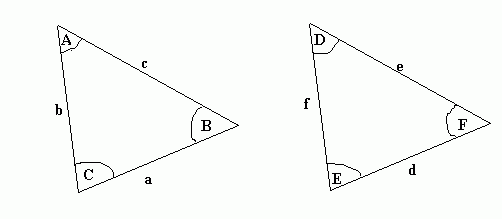
• All three sides of one triangle are the same length as all three sides of the other triangle (i.e. a = d, b = f and c = e below). If we know that this is true we write "SSS".
• Two of the angles and a side of one triangle are equal to the corresponding two angles and side of the other triangle (e.g. A = D, C = E and a = d) . For this we write "ASA".
• An angle between two sides of a triangle is equal to the corresponding angle in the other triangle and the sides in question are equal (e.g. C = E, b = f, a = d). We write "SAS".
• Two right angled triangles have the same hypotenuse and one other equal side.

Image

Congruency and Transformations

If a shape is translated, rotated or reflected, what we are left with will be congruent to what we started with. This is because a translation just moves a shape: it doesn't change the angles or the lengths of the sides. The same is true of a rotation. A reflection might change how a shape looks, but it doesn't change the lengths of any of the sides or the size of the angles.