Similar Triangles
This page covers Similar triangles.
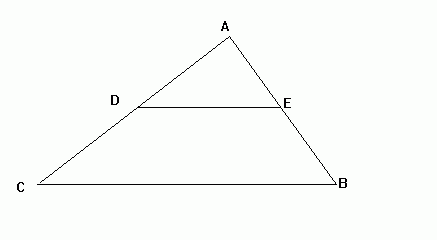
If CB and DE are parallel, the ratio of CD to DA and the ratio of BE to EA are equal. In other words, CD/DA = BE/EA . This is often a useful way of solving triangle problems and can be derived from the properties of similar triangles.
If two shapes are similar, one is an enlargement of the other. This means that the two shapes will have the same angles and their sides will be in the same proportion (for example, the sides of one triangle might all be 3 times the length of the sides of the other).
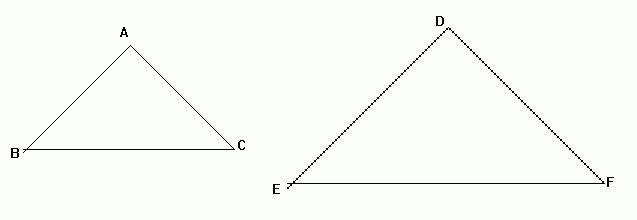
angle A = angle D
angle B = angle E
angle C = angle F
AB/DE = BC/EF = AC/DF = perimeter of ABC/ perimeter of DEF
Two triangles are similar if any of the following is true:
-
3 angles of 1 triangle are the same as 3 angles of the other
-
3 pairs of corresponding sides are in the same ratio
-
An angle of 1 triangle is the same as the angle of the other triangle and the sides containing these angles are in the same ratio.
Example
In the above diagram, the triangles are similar. EF = 6cm and BC = 2cm . What is the length of DE if AB is 3cm?
EF = 3BC, so DE = 3AB = 9cm.

