Sin, Cos and Tan

This section looks at Sin, Cos and Tan within the field of trigonometry.

A right-angled triangle is a triangle in which one of the angles is a right-angle. The hypotenuse of a right angled triangle is the longest side, which is the one opposite the right angle. The adjacent side is the side which is between the angle in question and the right angle. The opposite side is opposite the angle in question.

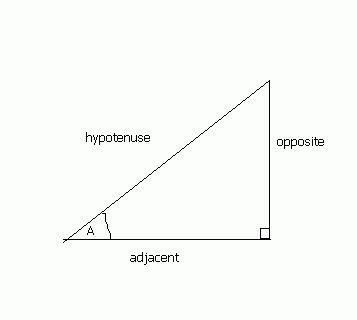
In any right angled triangle, for any angle:

The sine of the angle = the length of the opposite side

the length of the hypotenuse

The cosine of the angle = the length of the adjacent side

the length of the hypotenuse

The tangent of the angle = the length of the opposite side

the length of the adjacent side

So in shorthand notation:

sin = o/h cos = a/h tan = o/a

Often remembered by: soh cah toa

Example

Find the length of side x in the diagram below:

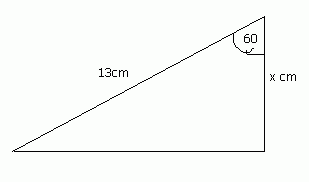
The angle is 60 degrees. We are given the hypotenuse and need to find the adjacent side. This formula which connects these three is:

cos(angle) = adjacent / hypotenuse

therefore, cos60 = x / 13

therefore, x = 13 × cos60 = 6.5

therefore the length of side x is 6.5cm.

This video will explain how the formulas work.

The Graphs of Sin, Cos and Tan - (HIGHER TIER)

The following graphs show the value of sinø, cosø and tanø against ø (ø represents an angle). From the sin graph we can see that sinø = 0 when ø = 0 degrees, 180 degrees and 360 degrees.

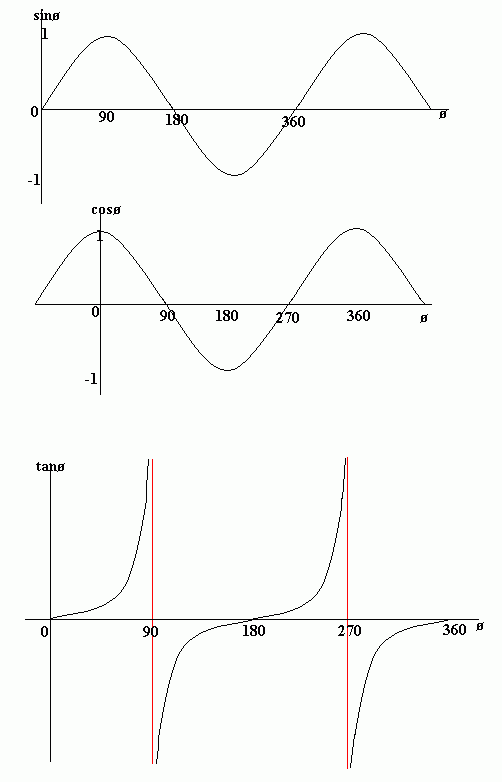
Note that the graph of tan has asymptotes (lines which the graph gets close to, but never crosses). These are the red lines (they aren't actually part of the graph).

Also notice that the graphs of sin, cos and tan are periodic. This means that they repeat themselves. Therefore sin(ø) = sin(360 + ø), for example.

Notice also the symmetry of the graphs. For example, cos is symmetrical in the y-axis, which means that cosø = cos(-ø). So, for example, cos(30) = cos(-30).

Also, sin x = sin (180 - x) because of the symmetry of sin in the line ø = 90.

Log in