Arithmetic and Geometric Sequences

This section of Revision Maths explains arithmetic and geometric number sequences in algebra.

Arithmetic Sequences

An arithmetic sequence is a sequence of numbers having a common first difference.

Taking the following sequence as an example

4 7 10 13 16

For any arithmetic sequence, the position to term formula is given by U_n = dn + (a-d) where a is the first term and d is the common difference. So in the above example U_n= 3n + (4-3), i.e. U_n= 3n + 1.

The next number in the above sequence will therefore be U₆ = 3 x 6 + 1 = 19.

The video below explains number sequences and how to find the nth term.

Geometric Sequences

In a geometric sequence you must multiply by a constant number (common ratio) r to go from one term to the next.

Taking the following example:

3 9 27 81 243

Each number is multiplied by 3 each time, giving us the common ratio of r = 3.

The term to term formula is U_n₊₁ = 3Uₙ with U₁ = 3.

The position to term formula is Uₙ = 3ⁿ.

If we take the following example:

Image

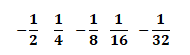
The common ratio r is ½

The term to term formula is U_n ₊₁ = - un with U₁ = ½

                                                                            2

The position to term formula is Uₙ = (-1/2)ⁿ