Working with Brackets

In maths you will need to be able to understand how to work with brackets. This section shows you the rules of using brackets and explains the box method.

To work with brackets follow these rules:

To multiply out single brackets, multiply the term outside the brackets by every term inside. Two examples are below:

5(2a – 6) = (5 x 2a) – ( 5x 6) = 10a – 30

3b(6b + 2q) = (3b x 6b) + (3b x 2q) = 18b² + 6bq

To multiply out double brackets, multiply every term in the first bracket by every term in the second bracket. For example:

(2y + 3) (y - 6) = (2y x y) + (2y x -6) + (3 x y) + (3 x -6)

= 2y² - 12y + 3y – 18

= 2y² - 9y – 18

When squaring brackets, always write out the expression in full to avoid making errors. For example:

(3y – 2)² = (3y – 2) (3y – 2) = 9y² - 6y – 6y + 4

= 9y² -12y + 4 (Note (3y -2)² is not equal to 9y² + 4).

Double brackets can also be multiplied out using a box method. Let’s take the following example.

(2y + 1) (3y – 2)

Image

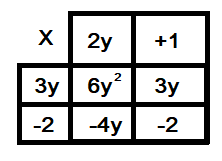
So (2y + 1) (3y – 2) = 6y² + 3y – 4y – 2

= 6y² - y – 2

Square brackets can also be multiplied out using the box method.

So if we wanted to expand (3 – 2b)²

Image

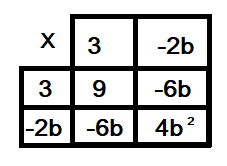
So (3 – 2b)² = 9 – 6b – 6b +4b²

= 9 – 12b + 4b²

To find out more about factorising view this video.