Circles, Sectors, and Arcs
In this guide, we will cover the key topics related to circles, including the diameter and radius, the circumference and area of a circle, and more advanced concepts such as arc length and sector area. Understanding these concepts is essential for Maths and will help you in solving various problems involving circles.
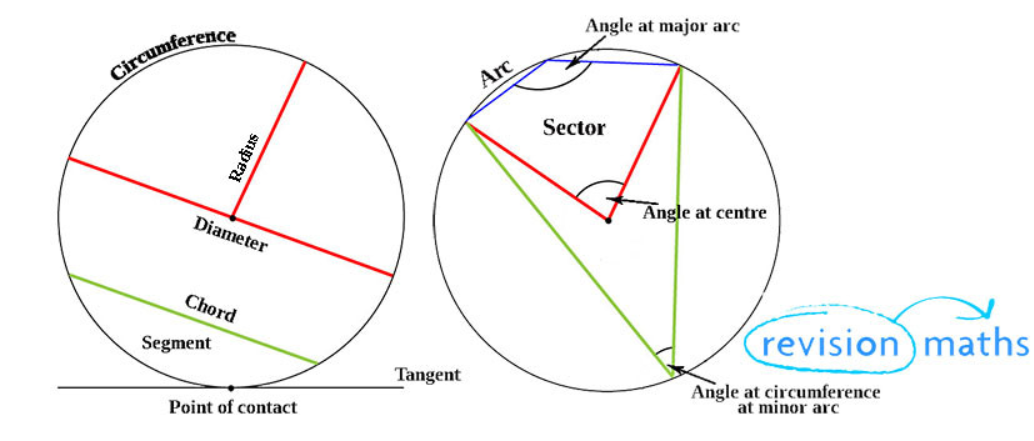
Diameter and Radius
- Radius: The radius is the distance from the centre of the circle to any point on its circumference. If you think of a wheel, the radius would be the distance from the centre of the wheel to the edge.
- Diameter: The diameter is the distance across the circle, passing through the centre. It is twice the length of the radius.
Formula:
$$\text{Radius} = \frac{\text{Diameter}}{2}$$
Formula:
$$\text{Diameter} = 2 \times \text{Radius}$$
Circumference of a Circle
The circumference is the distance around the edge of the circle, also known as the perimeter of the circle. The circumference can be found using the following formula:
$$C = \pi \times d$$
Where:
- $C$ is the circumference
- $\pi$( pi) is approximately 3.1416
- $d$ is the diameter of the circle
Alternatively, if you are given the radius (r), you can use the formula:
$$C = 2 \pi r$$
Example:
If the radius of a circle is 7 cm, the circumference would be:
$$C = 2 \times \pi \times 7 = 14 \pi \approx 43.98 \, \text{cm}$$
Area of a Circle
The area of a circle is the amount of space inside the circle. It can be calculated using the formula:
$$A = \pi r^2$$
Where:
- $A$ is the area
- $r$ is the radius of the circle
Example:
If the radius of a circle is 5 cm, the area would be:
$$A = \pi \times 5^2 = 25\pi \approx 78.54 \, \text{cm}^2$$
More Parts of a Circle
Chord
A chord is a straight line joining any two points on the circumference of the circle. The longest possible chord in a circle is the diameter.
Tangent
A tangent is a straight line that touches the circle at exactly one point. This point is called the point of tangency.
Sector
A sector of a circle is the region enclosed by two radii and the arc between them. It is essentially a "slice" of the circle.
- The area of a sector is calculated based on the fraction of the circle it occupies.
Segment
A segment is the region bounded by a chord and the arc that it cuts off.
Arc Length
The arc length is the distance along a portion of the circumference of the circle. To find the length of an arc, you need to know the angle subtended by the arc at the centre of the circle. The formula for the arc length is:
$$L = \frac{\theta}{360^\circ} \times 2 \pi r$$
Where:
- $L$ is the arc length
- $\theta$ is the angle in degrees
- $r$ is the radius of the circle
- $\pi$ is approximately 3.1416
Example:
If the radius of a circle is 10 cm and the angle subtended by the arc is 60°, the arc length would be:
$$L = \frac{60^\circ}{360^\circ} \times 2 \pi \times 10 = \frac{1}{6} \times 20 \pi \approx 10.47 \, \text{cm}$$
Sector Area
The area of a sector is the portion of the total area of the circle that is bounded by the two radii and the arc. The formula for the area of a sector is:
$$A_{\text{sector}} = \frac{\theta}{360^\circ} \times \pi r^2$$
Where:
- $A_{\text{sector}}$ is the area of the sector
- $\theta$ is the angle in degrees
- $r$ is the radius of the circle
- $\pi$ is approximately 3.1416
Example:
If the radius of a circle is 8 cm and the angle of the sector is 90°, the area of the sector would be:
$$A_{\text{sector}} = \frac{90^\circ}{360^\circ} \times \pi \times 8^2 = \frac{1}{4} \times 64 \pi \approx 50.27 \, \text{cm}^2$$
This video explains circle theorems in more detail.
Summary of Key Formulas
- Radius to Diameter: $d = 2r$
- Diameter to Radius: $r = \frac{d}{2}r$
- Circumference: $C = 2 \pi r$ or $C = \pi d$
- Area of a Circle: $A = \pi r^2$
- Arc Length: $L = \frac{\theta}{360^\circ} \times 2 \pi r$
- Sector Area: $A_{\text{sector}} = \frac{\theta}{360^\circ} \times \pi r^2$
With these formulas and understanding of key circle concepts, you’ll be well-prepared to tackle any higher-tier GCSE maths problems involving circles, sectors, and arcs.

