Equation of a Circle
This page looks at equations of a circle and completing the square.
The equation of a circle with centre (a, b) and radius r is (x - a)2 + (y - b)2 = r2.
This is a result of Pythagoras' Theorem
Image
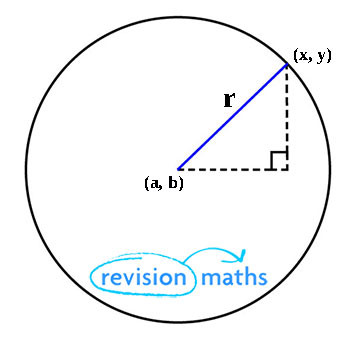
For example, the equation of a circle with centre (3, 0) and radius 4 units is (x – 3)2 + y2 = 16.
The General Form of the equation of a circle is x2 + y2 + 2gx +2fy + c = 0.
The centre of the circle is (-g, -f) and the radius is √(g2 + f2 - c).
Completing the square
Given a circle in the general form you can complete the square to change it into the standard form.
More on this can be found on the Quadratic Equations page Here.
Circle Properties
You need to remember circle properties found Here

