Properties of Polygons

A Polygon is a 2D shape which is made up of straight line segments. A regular polygon has all sides and angles equal (e.g. a square is a regular quadrilateral). A triangle with all sides and angles equal is known as an equilateral triangle.

Polygons are named after the number of sides they have.

Three Sides – Triangle

Four Sides – Quadrilateral (e.g. square or rectangle)

For more on the properties of quadrilaterals click here.

Five Sides – Pentagon

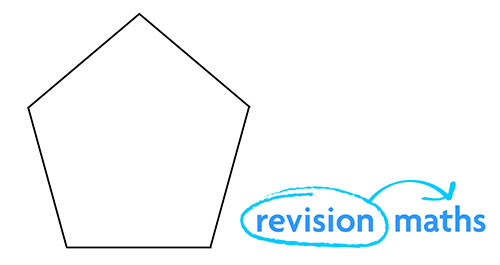
In the UK this is the shape used for a 50 pence coin.

Six Sides – Hexagon

Seven Sides - Heptagon

Eight Sides – Octagon

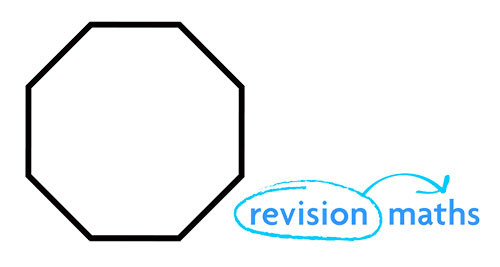
Nine Sides – Nonagon

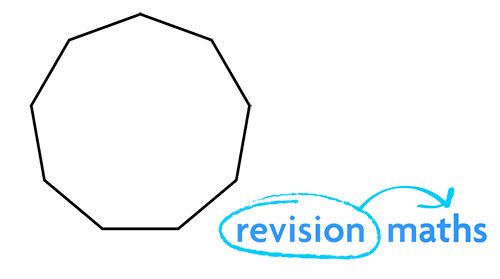
Ten Sides – Decagon

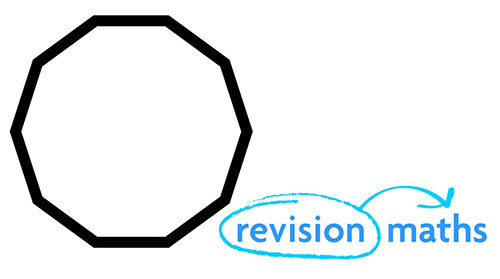
Angles of Polygons

All polygons have both internal angles and external angles. The polygon’s external angle is the angle of one side extended and the next side.

The external angles of a polygon will always add up to 360⁰.

You can calculate the internal angles of a polygon using either of the methods below:

Method 1: Assume the polygon is regular.

Begin by working out the size of each external angle. Then use the angles on a straight line rule to work out each angle. Finish up by adding up all the total angles.

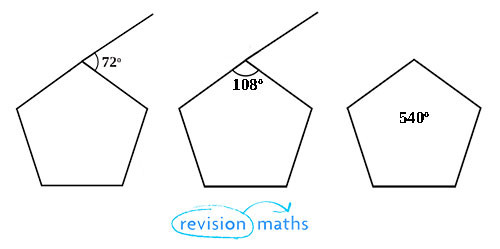
In the example above we are using a pentagon. We therefore divide 360 by 5 to give us an external angle of 72⁰. If we take 72 from 180 we get 108⁰. We times this by 5 to give us 540⁰.

You can find more examples on Revision Maths on our Angles Page.

Method 2: Divide the polygon into triangles.

Once you have divided the polygon into triangles you can use the angle sum of a triangle rule to work out the sum of all of the angles. If the shape is regular you can then calculate the size of each angle by dividing the sum of all angles by the number of sides on the shape.

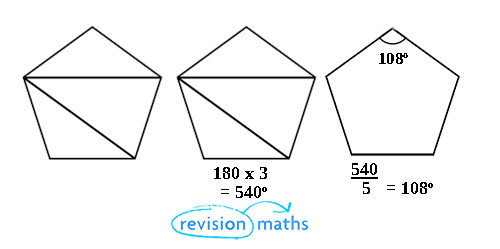
In the example above we just times 180 by 3 (as we can fit 3 triangles into the pentagon). This also gives us 540⁰. You then then divide this by 5 to give us 108⁰ this is therefore the size of each internal angle.

The video below looks at the properties of triangles and quadrilaterals.

Log in