Rates of Change
Calculating rates of change is an important part of the GCSE Maths curriculum for students studying the higher paper.
To calculate rates of change in your exam you will need to be able to interpret graphs. To refresh your memory of Gradients and Graphs click here.
The graph below shows the cost of three different mobile phone tariffs.
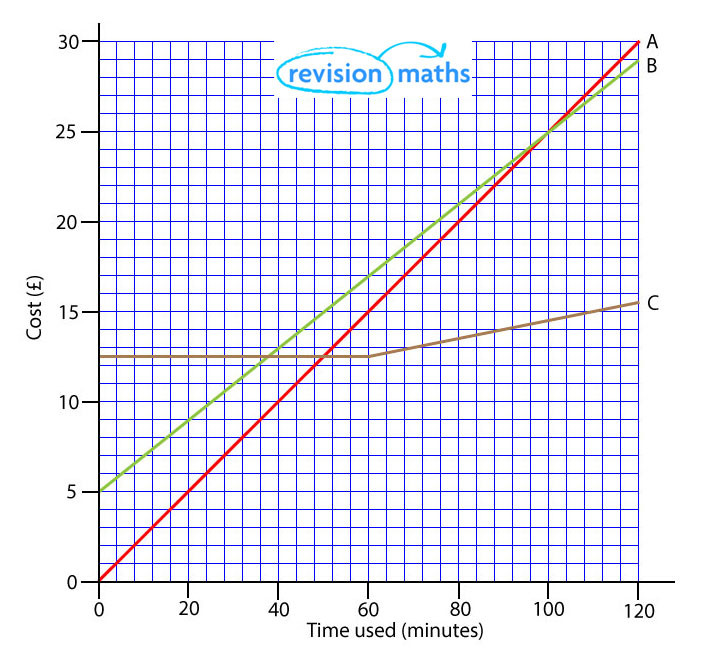
Line A shows a direct proportion. The gradient of the line represent the rate of change.
The formula is therefore the change in the y axis divided by the change in the x axis.
In this example that equals 10 ÷ 40 = 0.25. This represents a charge of 25p per minute and shows a constant proportion.
Line B shows a fixed charge of £5 regardless of how many calls are made. The gradient is 20 ÷ 100 = 0.2 or 20p per minute.
Line C shows a fixed charge of £12.50, with no call charges up to 60 minutes. After 60 minutes the gradient is 3 ÷ 60 = 0.05 0r 5p a minute.
You can use the graph to see which tariff represents best value for you. After about 55 minutes this would be tariff C, if you use fewer minutes than this it would be tariff A. Tariff B is therefore never the best value option.
Repetitive rate of change
With repetitive rates of change the percentage change is applied more than once. You therefore have to calculate one step at a time.
For example, if a business buys a computer for £1,000. In the first year it depreciates by 25%, the next year it loses 20% of its value and then 10% every year after that.
You may then be asked how much is the computer worth after 3 years? To calculate this you can use one of two methods.
Method 1: Step by Step:
Lose 25% so worth 75% after year one.
75% of 1,000 = 0.75 x 1000 = £750
Then 80% of 750 = 0.80 x 750 = £600
Then 90% of 600 = 0.90 x 600 = £540
So the computer is worth £540 after 3 years.
Method 2: Using multipliers:
Lose 25% so worth 75%
Lose 20% so worth 80%
Lose 10% so worth 90%
0.75 x 0.80 x 0.90 = 0.54
Then 0.54 x 1000 = £540
For more information on Ratios, proportion and rates of change click here.
